Аннотация

В данной работе сделана попытка дать подробное описание проблемы адаптации алгоритмов распознавания к входным символам на основе анализа статистики. Обоснована целесообразность применения адаптивной технологии, как подхода обеспечивающего существенное увеличение качества распознавания. Приведена математическая модель адаптивного распознавания. Предложена схема синтеза традиционных и адаптивных алгоритмов распознавания. Затронут широкий круг вопросов связанных с техническими проблемами возникающими при реализации.

Обзор подходов к распознаванию символов

В случае, когда речь идет о распознавании печатных символов следует упомянуть, что почти бесконечное разнообразие печатной продукции изготавливается при помощью ограниченного набора оригиналов символов, которые группируются по стилю (набору художественных решений), который отличает данную группу от других. Одна группа, включающая все алфавитные знаки, цифры и стандартный набор служебных символов, называется гарнитурой. Однако в широком кругу людей, имеющих дело с производством различного рода документации, утвердилось другое название гарнитуры - шрифт; этого термина мы и будем придерживаться в дальнейшем.

Итак любой печатный текст имеет первичное свойство - шрифты, которыми он напечатан. С этой точки зрения существуют два класса алгоритмов распознавания печатных символов: шрифтовой и безшрифтовый (omnifont). Шрифтовые или шрифтозависимые алгоритмы используют априорную информацию о шрифте, которым напечатаны буквы. Это означает, что программе ОРС  должна быть предъявлена полноценная выборка текста, напечатанного данным шрифтом. Программа измеряет и анализирует различные характеристики шрифта и заносит их в свою базу эталонных характеристик. По окончании этого процесса шрифтовая программа оптического распознавания символов (ОРС) готова к распознаванию данного конкретного шрифта. ( В последнее время, задачи при решении которых требуется обучение стали ассоциироваться с применением нейронных сетей [6], однако здесь развивается технология не использующая НС). Этот процесс условно можно назвать обучением программы. Далее обучение повторяется для некоторого множества шрифтов, которое зависит от области применения программы.

n    Алгоритм должен заранее знать шрифт, который ему  представляют для распознавания, т.е. он должен хранить в базе различные характеристики этого шрифта. Качество распознавания текста, напечатанного произвольным шрифтом, будет прямо  пропорционально корреляции характеристик этого шрифта со шрифтами, имеющимися в базе программы. При существующем богатстве печатной продукции в процессе обучения  невозможно охватить все шрифты и их  модификации. К примеру, Полиграфбуммаш СССР в свое время стандартизировал около 15-20 различных шрифтов, в современных компьютерных системах верстки документов используется более 100 шрифтов. Другими словами, этот фактор  ограничивает универсальность таких алгоритмов.

n    Программа, основанная на шрифтовом алгоритме распознавания символов, требует от пользователя специальных знаний о шрифтах вообще, об их группах и отличиях друг от друга, шрифтах, которыми напечатан документ, пользователя. Отметим, что в случае, если бумажный документ не создан самим пользователем, а пришел к нему извне, не существует регулярного способа узнать с использованием каких шрифтов этот документ был напечатан. Фактор необходимости специальных знаний сужает круг потенциальных пользователей и сдвигает его в сторону организаций, имеющих в штате соответствующих специалистов.

С другой стороны, у шрифтового подхода имеется преимущество, благодаря которому его активно используют и, по-видимому, будут использовать в  будущем. А именно,  имея детальную априорную информацию о символах, можно построить весьма точные и надежные алгоритмы распознавания. Вообще, при построении шрифтового алгоритма распознавания (в отличие от безшрифтового, о чем будет сказано ниже)  надежность распознавания символа является интуитивно ясной и математически точно выразимой величиной. Эта величина определяется как расстояние в каком-либо метрическом пространстве от эталонного символа, предъявленного программе в процессе обучения, до символа, который программа пытается распознать.

Второй класс алгоритмов - безшрифтовые или шрифтонезависимые, т.е. алгоритмы, не имеющие априорных знаний о символах, поступающих к ним на вход. Эти алгоритмы измеряют и анализируют различные характеристики (признаки), присущие буквам как таковым безотносительно шрифта и  абсолютного размера (кегля), которым они напечатаны [3]. В предельном случае для шрифтонезависимого алгоритма процесс обучения может отсутствовать. В этом случае характеристики символов измеряет, кодирует и помещает в базу программы  сам человек. Однако на практике, случаи,  когда такой путь исчерпывающе решает поставленную задачу, встречаются редко. Более общий путь создания базы характеристик заключается в обучении программы на выборке реальных символов.

К недостаткам данного подхода можно отнести следующие факторы:

n     Реально достижимое качество распознавания ниже, чем у шрифтовых алгоритмов. Это связано с тем, что уровень обобщения при измерениях характеристик символов гораздо более высокий, чем в случае шрифтозависимых алгоритмов. Фактически это означает, что различные допуски и огрубления при измерениях характеристик символов для работы безшрифтовых алгоритмов могут быть в 2-20 раз больше  по сравнению с шрифтовыми.

n    Следует считать большой удачей, если безшрифтовый алгоритм обладает адекватным и физически обоснованным, т.е. естественно проистекающим из основной  процедуры алгоритма, коэффициентом надежности распознавания. Часто приходится мириться с тем, что оценка точности либо отсутствует, либо является искусственной. Под искусственной оценкой подразумевается то,  что она существенно не совпадает с вероятностью правильного распознавания, которую обеспечивает данный алгоритм.

Достоинства этого подхода тесно связаны с его недостатками. Основными  достоинствами являются следующие:

n    Универсальность. Это означает с одной стороны применимость этого подхода в случаях, когда потенциальное разнообразие символов, которые могут поступить на вход системы, велико. С другой стороны, за счет заложенной в них способности обобщать, такие алгоритмы могут экстраполировать накопленные знания за пределы обучающей выборки, т.е. устойчиво распознавать символы, по виду далекие от тех, которые присутствовали в обучающей выборке.

n    Технологичность.  Процесс обучения шрифтонезависимых алгоритмов обычно является более  простым и интегрированным в том смысле, что обучающая выборка не фрагментирована на различные классы (по шрифтам, кеглям и т.д.). При этом отсутствует необходимость поддерживать в базе характеристик различные условия совместного существования этих классов (некоррелированность, не смешиваемость, систему уникального именования и т.п.). Проявлением технологичности является также тот факт, что часто удается создать почти полностью автоматизированные процедуры обучения.

n    Удобство в процессе использования программы. В случае, если программа построена на шрифтонезависимых алгоритмах, пользователь не  обязан знать что-либо о странице, которую он хочет ввести в компьютерную память и уведомлять об этих знаниях программу. Также упрощается пользовательский интерфейс программы за счет отсутствия набора опций и диалогов, обслуживающих обучение и управление базой характеристик. В этом случае процесс распознавания можно представлять пользователю как "черный ящик” (при этом пользователь полностью лишен возможности управлять или каким-либо образом модифицировать ход процесса распознавания). В итоге это приводит к расширению круга потенциальных пользователей за счет включения в него людей обладающих минимальной компьютерной грамотностью.

Выше рассматривались особенности, достоинства и недостатки двух подходов к созданию алгоритмов ОРС. Из обзора следует, что достоинства и недостатки обоих подходов определяются  одними и теми же свойствами алгоритмов: большей либо меньшей степенью универсальности, степенью достижимой точности распознавания и т.п. Сравнительные недостатки и достоинства обоих подходов сведены в таблицу.

Рассмотрение обоих подходов в сравнении друг с другом приводит к целесообразности их объединения. Цель объединения очевидна - получить метод, совмещающий  одновременно универсальность и технологичность безшрифтового подхода и высокую точность распознавания шрифтового. Предпосылками для исследования в этом направлении послужил следующий круг идей и фактов. Любой алгоритм распознавания символов становится применим на практике при качестве распознавания  94-99%. "Дожимание” последних процентов, т.е. окончательная доводка алгоритма всегда является трудоемкой и дорогостоящей работой. Внутри сферы распознавания символов любой алгоритм имеет свою специфичную область действия, для которой он разработан и в которой проявляет себя наилучшим образом. В целом, путь увеличения качества распознавания лежит не в изобретении  сверхинтеллектуального алгоритма, который заменит собой все остальные, а в  комбинировании нескольких алгоритмов, каждый из которых сам по себе прост и обладает эффективной вычислительной процедурой. При комбинировании различных алгоритмов важно, чтобы они опирались на независимые источники информации о символах. В случае, если два алгоритма работают над сильно коррелированными между собой данными, то вместо увеличения качества распознавания будет увеличиваться суммарная ошибка. С другой стороны, знания о распознанных символах должны накапливаться и использоваться в последующих шагах процесса распознавания. Более того, как окончательный критерий можно использовать точный шрифтозависимый алгоритм, база характеристик которого построена прямо в процессе работы ("на лету”) по результатам предыдущих шагов распознавания. Метод, обладающий указанным выше свойством, будем называть адаптивным распознаванием, т.к. он использует динамическую настройку (адаптацию) на конкретные входные символы.

Математическая модель адаптивного распознавания

В модели приняты следующие допущения:

n    Символы обучающей выборки и материала распознавания принадлежат единственному шрифту. Обобщение этой модели на случай произвольного количества шрифтов требует отдельного исследования.

n    Все символы внутри одного цикла адаптивного распознавания имеют одинаковую степень искажений, вносимых процессами печати и сканирования. Это предположение отвечает ситуации, когда единицей цикла является одна страница текста

n    Имеется некий готовый шрифтонезависимый алгоритм с определенным качеством распознавания. В данном случае не важно, откуда взялся этот алгоритм, каким образом он анализирует символы, его особенности и детали реализации.

n    ежду различными кластерами безусловно должен быть учтен при моделировании адаптивного распознавания.

Модель охватывает два ключевых этапа адаптивного распознавания: кластеризация символов обучающей выборки и дораспознавание. Модель создается с целью получения аппарата, позволяющего оценить теоретический предел качества распознавания и надежности при заданных параметрах первичного распознавания и меры искаженности символов. Ниже следует перечисление параметров модели.

P- качество распознавания, полученное на этапе первичного распознавания

s- мера искаженности символов, дает числовое выражение количеству случайных изменений в конфигурации пикселов среди экземпляров символов, обозначающих одну и ту же букву алфавита.

F- финальное качество распознавания достижимое с помощью шрифтозависимого алгоритма адаптированного  к данной выборке символов.

V- надежность распознавания символа; V = f ( x,P ), где x-расстояние от данного символа до центра кластера(идеального символа). Функция f является частью конкретного алгоритма вычисления расстояния между символом и кластером. Зависимость надежности от расстояния до идеала указывает на интуитивно очевидную связь между надежностью и отличием символа от идеала. Зависимость надежности от качества первичного распознавания отражает тот факт, что при зафиксированном х  надежность может быть различной в зависимости от качества материала из которого составлен кластер.

 Предположим выбрана метрика, т.е. функция отображающая отличия между символом и кластером в действительное положительное число (расстояние). Основное положение модели заключается в том, что расстояние от символа пришедшего на распознавание до кластера есть нормально распределенная случайная величина с плотностью вероятности.

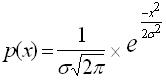
Тогда по заданной минимальной допустимой надежности Vmin   вычислим максимальное расстояние Xm на которое символ может отклониться от кластера и при котором V >= Vmin 

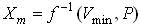
Далее по определению функции распределения [2] получаем

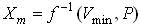
Это равенство дает ответ на вопрос каким будет качество распознавания при заданных надежности и мере искаженности символов.  Наоборот, измерив на представительной выборке качество распознавания, можно по таблице [5] выяснить с какой надежностью получен этот результат.

  Большой практический интерес представляет измерение величины s - среднеквадратичного отклонения; т.к. она придает числовое выражение важному понятию - "качество текста”. В этой модели s обретает конкретный физический смысл - описывает вариации которые возникают в конфигурации пикселов, описывающих оригинал символа, в процессах печати и сканирования. Применение шкалы основанной на мерах рассеяния подобной вышеупомянутой найдет применение в различных аспектах распознавания символов. Перечислим наиболее важные:

 n    Верификация результатов кластеризации. Имеется ввиду, что кластер с рассеянием существенно отличным от среднего по выборке должен вызывать подозрение и являться кандидатом на дополнительную проверку.

 n    Динамическая настройка различных пороговых констант, управляющих распознаванием.

 n    Экстремальные значения s могут указывать на ситуацию в которой сама адаптация к данной выборке является не выгодной ибо необходимая статистическая информация в ней отсутствует.

 n    Автоматическая селекция документов для дальнейшей обработки.

Интересным с практической точки зрения  является вопрос о том, насколько близки параметры реального кластера к параметрам разработанной здесь модели. Ниже приводится оценка, позволяющая определить как с ростом количества символов параметры кластера сходятся к теоретическим.

 Возьмем произвольную ячейку кластера. Пусть p